Imaginez que vous vouliez déterminer si la souris est un animal capable d’apprendre une tâche comportementale X. Vous avez déjà testé 19 animaux et arrivez à la conclusion qu’elle n’en est pas capable. Tout à coup, après que le 20ème animal a passé la tâche, vous changez radicalement d’opinion et vous concluez que la souris est capable d’apprendre cette tâche X. Qu’est-ce que cette dernière souris a d’aussi spécial ? Rien de particulier en réalité, mais les données de cette souris ont fait passer la valeur-p de votre test statistique au-dessous du soit disant « seuil de significativité de 5% » (disons de p=0.070 à p=0.045). La différence de 0.025 point d’un paramètre aussi fluctuant que la valeur-p https://www.ncbi.nlm.nih.gov/pubmed/24220629 a fait basculer votre opinion sur les souris que nous pourrions caricaturer en « Elles sont bêtes » à « Elles sont intelligentes » .
Qu’est-ce que ce seuil de 5% a d’aussi magique ? Le seuil de significativité est ce que les statisticiens appellent le risque α ; c’est le risque maximal que vous êtes prêt à courir en considérant un résultat comme ‘positif’ (la différence existe) lorsqu’en réalité le résultat est négatif (il n’y a pas de différence). C’est donc le risque de produire un faux positif. La valeur de 5% a été choisie de manière arbitraire par la communauté scientifique sur proposition du statisticien Fisher. Elle aurait tout aussi bien pu être de 0.5%, comme l’a récemment proposé un groupe de chercheurs afin de réduire le problème de reproductibilité des données scientifiques (https://www.nature.com/articles/s41562-017-0189-z).
Cependant d’autres scientifiques considèrent que le problème n’est pas la valeur de ce seuil de significativité, mais son existence même https://arxiv.org/abs/1709.07588 https://peerj.com/preprints/2921/ . Au-delà d’argumentations purement statistiques (que nous n’avons pas les compétences de discuter), les critiques principales de ces auteurs sur le seuil de significativité sont les suivantes :
- Il amène, de manière plus ou moins consciente, à une vision dichotomique de la réalité (la souris bête ou intelligente de l’exemple précédent).
- Il focalise l’attention sur une des multiples informations que l’on peut tirer de l’analyse de données expérimentales : la valeur-p, rendant secondaire, voire inutile, l’interprétation des autres éléments. A cela s'ajoute parfois une confusion autour de la signification de la p-value pouvant amener à des conclusions grossièrement fausses (exemple : p-value petite = effet important).
- Il peut être un des moteurs de l’inconduite scientifique, la crainte que les pairs ne jugent les résultats intéressants que s’ils sont « significatifs » pouvant mener à des pratiques de falsification plus ou moins consciente des résultats.
En partant de là, certains chercheurs proposent d’abandonner l’utilisation du seuil de significativité, de considérer la valeur-p mais en s’intéressant à sa valeur même et non pas à sa position par rapport à un seuil, et de prendre en compte d’autres paramètres dans l’interprétation des résultats expérimentaux. Ainsi, au-delà du regard global qu’il faut porter sur les données expérimentales, les auteurs suggèrent d’inclure :
- la plausibilité de l’hypothèse testée,
- la plausibilité des mécanismes sous-jacents à l’effet observé dans l’échantillon expérimental,
- la qualité des données et de l’approche expérimentale,
- le contexte de l’étude et la question scientifique.
Voici une mise en situation permettant de résumer la vision décrite ci-dessus :
Nous comparons l'action anti-hypertensive de quatre molécules A, B, C et D.
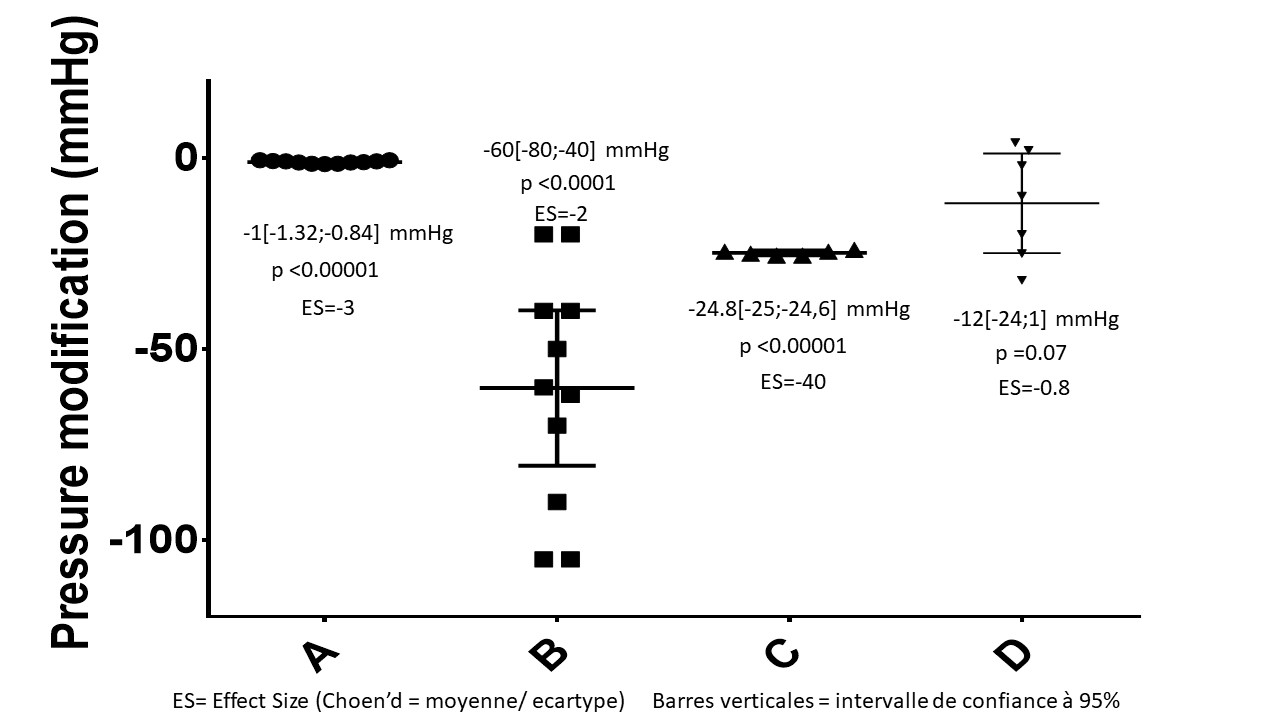
Si nous nous limitons à une évaluation basée uniquement sur la valeur-p, alors l’interprétation serait : A, B et C sont des antihypertenseurs efficaces (p < 0.05), contrairement à D (p > 0.05).
Par contre si nous jetons un regard sur les données expérimentales et que nous les considérons dans un contexte thérapeutique, alors l’interprétation est bien différente : L’effet produit par le traitement A, bien que cohérent, est si petit qu’il peut être considéré comme négligeable. Le traitement B produit une réduction réelle de la pression, mais la grande variabilité de son effet le rend peu prévisible et potentiellement dangereux dans un contexte thérapeutique. Le traitement C produit quant à lui très probablement une réduction réelle de la pression avec un effet important et constant ; il est donc apparemment efficace pour traiter l’hypertension. Enfin, le traitement D semble avoir des effets antihypertenseurs potentiellement intéressants, et la variabilité de l’effet, plus petit que celle de B, le rend exploitable pour un traitement thérapeutique. Cela nécessiterait cependant des investigations supplémentaires.
Enfin, si nous considérons la plausibilité du résultat, nous pouvons douter de la véridicité des données observées avec la molécule C (un effet aussi consistant avec ES=-40, est-il réellement compatible avec la variabilité intrinsèque aux systèmes biologiques ?).
En conclusion, en prenant en compte l’ensemble de ces considérations, nous arrivons à une interprétation diamétralement opposée à celle obtenue en considérant uniquement la valeur-p : Dans un contexte thérapeutique, A est un anti-hypertenseur inefficace, B est un anti-hypertenseur efficace mais dont l’effet est imprévisible, C est non plausible, et D, bien que potentiellement efficace mérite une investigation supplémentaire.

Comments